Phillies, George DJ. Elementary lectures in statistical mechanics. Springer Science & Business Media, 2000. Guha, E. Statistical Mechanics: An Introduction. Alpha Science International, 2008. https://iopscience.iop.org/article/10.1088/2632-2153/abc9fe

Ensemble

为了定义系统,取整个世界,或者整个世界的模型, 的一部分来作为所谓的system.而system以外的部分是bath. 对于这个系统,如果希望能够应用在统计物理学中,则必须满足“能够有完整的对其微观状态的描述”此条件(any system that can be treated by statistical mechanics can be given a complete, microscopic description.).例如,对于牛顿系统,一个完整的对微观状态的描述可以是:每个原子的坐标以及动量.对于量子系统,则可以是所有basis vector的幅度和相.对于system必须有完整的表述,但是对于bath的话,无所谓

State: 通过微观的变量(例如对于传统系统是原子坐标和动量,对于quantum system: amplitude and phased for each basis vector)来描述微观状态,那么当所有微观变量取了一个值之后,得到了一个state.每个state都对应一个唯一的微观变量们的取值
number of microstate: $\Omega$ 大omega是满足某个条件的所有state的数量,比如NVE ensemble中满足N=1,V=2,E=3的state总共有100个,则为 $\Omega_{(N=1,V=2,E=3)}=100$
entropy: 在NVE ensemble中,entropy满足 $S=k_B \Omega(N,V,E)$
Ensemble: 指这个系统所有unique state的集合. 每个state都是这个ensemble的element. 一般情况下ensemble都是在对系统施加了某个限定条件之后的state集合.(NVT之类的)
element of ensemble: 一个allowed state, 用来组成ensemble
Mechanical Variable: a function whose value can be calculated from the microscopic description of a single element of an ensemble.即可以通过element计算出来的物理性质,比如压强,自由能,动能,熵…
ensemble average: 对于某个系统,将其复制许多份,对于每个复制进行观察,这些系统会处于不同的state,对于所有这些复制体的mechanical variable进行观测,取平均,是ensemble average
phase space 例如,单个粒子具有position vector和canonically conjugate momentum vector. 投影到cartesian space这两个vector可以表示为$x,y,z,p_x,p_y,p_z$,即6个坐标.对于含有这6个坐标轴的空间,此空间中的一个点可以独特地定义一个系统的state. 对于含有N个粒子的系统,则有6N个坐标.此6N个坐标组成的space就是phase space.
phase point 在phase space中的一个点,这个点对应的是一个state. 一般写作 $\Gamma=(r^N,p^N)$ 例如一个只含有一个粒子的系统,此粒子位于(1,2,3),具有4,5,6的动能则 $\Gamma=(1,2,3,4,5,6)$ 此$\Gamma$点,即phase point,对应了这个系统的一个state

types of ensemble

microcanonical ensemble:NVE

因为E是固定的,所以stastistical weight是一个常数

如果严格要求E=E0,成为surface ensemble
如果考虑quantum system,有时候能量不是连续的,所以保持E不变是比较难以实施的(具体在P33),所以此时变为quantum microcanonical ensemble,要求E保持在$E_0+\delta E$此极小范围内. 对于一个仅固定了N和V的系统,其能量可以从0到正无穷,microcasnonical ensemble取其中所有满足E=E0(surface ensemble)或者$E_0+\delta E$(quantum)此条件的state(element)组成ensemble

canonical ensemble:NVT

指NVT ensemble,即在固定粒子数量,体积,温度情况下的ensemble/state集合.所有允许的state之间NVT都是一样的

stastistical weight是$W_j=Ce^{-\frac{E_j}{k_BT}}$
从而常数C: $C=\frac{1}{\sum_j e^{-\beta E_j}}$
Probability Distribution: $P(E=E_j)=\frac{e^{-\beta E_j}}{\sum_j e^{-\beta E_j}}$
partition function: $Z={\sum_j e^{-\beta E_j}}$

grand canonical ensemble: $\mu VT$

可以理解为对许多个N不一样但是VT一样的canonical ensemble的集合中,取其中$\mu = \mu_0$的所有element组成一个ensemble 或者说对于所有满足$V=V_0, T=T_0$而N随意取值(0~正无穷)的canonical ensemble,其组成一个canonical ensemble 的集合,对于所有满足了mu的element,提取出来组成grand canonical ensemble

isothermal-isobaric ensemble: NTP

isodynamic-polythermal ensembleL NVE, 与microcanonical ensemble不同之处在于其stastistical weight的定义不一样

MLIP

https://iopscience.iop.org/article/10.1088/2632-2153/abc9fe MACHINE learning potential: moment tensor potential

设定一个例子:

一个Na原子(编号1,坐标0,0,0),周围有两个O原子(编号23,坐标010,002)和一个P原子(编号4,坐标110) mtp中cutoff min=0.8, cutoff max=2.5

Neighbor: 周围环境:由$n_i$此集合描述

\[n_i=[z_i,z_j,r_{ij}]\]

例如对于Na原子

\[n_1=[z_1,z_2,r_{12},z_3,r_{13},z_4,r{14}]=[11,8,(0,1,0),8,(0,0,2),15,(1,1,0)]\]

z1是Na的原子序数11

Radial basis function:

\[Q^{\beta}(|r_{ij}|)= \phi^{\beta}(R_{cut}-r_{ij}^2)\space when\space |r_{ij}|<R_{cut}\] \[Q^{\beta}(|r_{ij}|)= 0 \space when\space |r_{ij}|>R_{cut}\]

其中phi是在$[R_{min},R_{cut}]$区间上的chebyshev polynomials,beta是chebyshev polynomial的级数 https://en.wikipedia.org/wiki/Chebyshev_polynomials

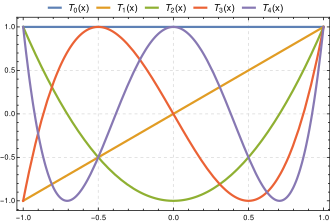
而乘以了$(R_{cut}-r_{ij}^2)$之后长成这个样子：

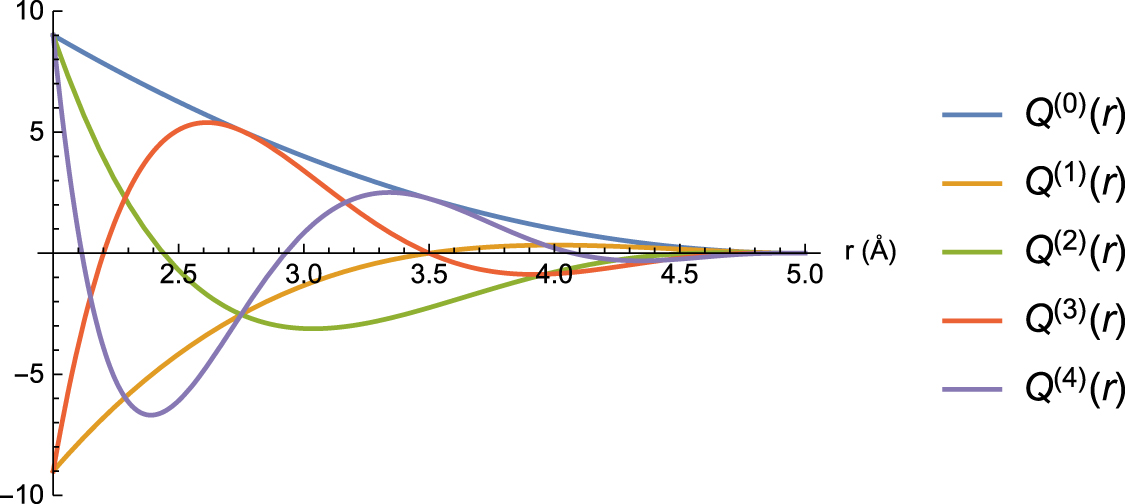cite from https://iopscience.iop.org/article/10.1088/2632-2153/abc9fe

\[Q^{0}(|r_{ij}|)= (R_{cut}-|r_{ij}|)^2=(2.5-|r_{ij}|)^2\] \[Q^{0}(|r_{ij}|=R_{cut})= 0\] \[Q^{0}(|r_{ij}|=R_{min})= (R_{cut}-|r_{ij}|)^2=(2.5-0.8)^2=2.89\]

\[Q^{1}(|r_{ij}|)= (\frac{2r_{ij}-R_{cut}-R_{min}}{R_{cut}-R_{min}})(R_{cut}-|r_{ij}|)^2=(\frac{2r_{ij}-3.3}{1.7})(2.5-|r_{ij}|)^2\] \[Q^{1}(|r_{ij}|=R_{cut})= (\frac{2R_{cut}-R_{cut}-R_{min}}{R_{cut}-R_{min}})(R_{cut}-R_{cut})^2=(R_{cut}-R_{cut})^2=0\] \[Q^{1}(|r_{ij}|=R_{min})= (\frac{2R_{min}-R_{cut}-R_{min}}{R_{cut}-R_{min}})(R_{cut}-|r_{ij}|)^2=-(R_{cut}-R_{min})^2=-2.89\]

\[Q^{2}(|r_{ij}|)= [2(\frac{2r_{ij}-R_{cut}-R_{min}}{R_{cut}-R_{min}})^2-1](R_{cut}-|r_{ij}|)^2\] \[Q^{2}(|r_{ij}|=R_{cut})= (2*(-1)^2-1)(R_{cut}-R_{cut})^2=(R_{cut}-R_{cut})^2=(R_{cut}-R_{cut})^2=0\] \[Q^{2}(|r_{ij}|=R_{min})= (2*1^2-1)(R_{cut}-|r_{ij}|)^2=(R_{cut}-R_{min})^2=2.89\]

更高形式参考wikipedia的第一类切比雪夫多项式

Radial part, 由Nq个radial basis function组合产生

$f_{\mu}(n_{ij})=f_{\mu}(|r_{ij},z_i,z_j|)=\sum^{N_Q}_{\beta=1}c^{\beta}_{\mu,z_i,z_j}Q^{\beta}(|r_{ij}|)$

$N_Q$是beta/切比雪夫不等式的最高级数

c的上标beta是每个radial basis function的系数。示例对于Na-P,当$N_Q=1$，

\[f_{\mu}(Na-P)=f_{\mu}(|r_{Na,P},Na,P|)=\sum^{2}_{\beta=1}c^{\beta}_{\mu,Na,P}Q^{\beta}(|r_{Na,P}|)\] \[=c^{0}_{\mu,Na,P}(2.5-|r_{Na-P}|)^2+c^{1}_{\mu,Na,P}(\frac{2|r_{Na-P}|-3.3}{1.7})(2.5-|r_{Na-P}|)^2\]

里面c对应的是trained mtp文件中的一行radial_coeffs，beta分别对应这行的每个数。如果Nq=8 （展开8个chebyshev polynomial），则radialcoeff每行就有8个

在MLIP的软件包里面给的所有的untrained potential里面默认的Nq=8

Angular part

$angular_v=r_{ij}\otimes r_{ij} \otimes ....(v \space times)$

对于neighbor求n次外积(outer product)

v=0, angular=1 v=1, $angular=r_{ij}=(x_{ij},y_{ij},z_{ij})$ v=2 看文章,是3*3矩阵看起来是个与v相关的tensor?

Moment tensor:

moment tensor是组合angular part和radial part，然后再遍历所有种类的neighbor

\[M_{\mu,v}(n_i)=\sum_j f_{\mu}(|r_{ij}|)*angular\]

需要注意的是，moment tensor可能是标量，也可能是矢量，比如

$M_{0,0}=\sum_j f_{0}(|r_{Na,j}|)*1=[c^{0}_{0,Na,P}(2.5-|r_{Na-P}|)^2+c^{1}_{0,Na,P}(\frac{2|r_{Na-P}|-3.3}{1.7})(2.5-|r_{Na-P}|)^2]+[Na-O]+...=[c^{0}_{0,Na,P}(2.5-1.414)^2+c^{1}_{\mu,Na,P}(\frac{2.828-3.3}{1.7})(2.5-1.414)^2]+....$ 这个就是个标量

然而比如当v=1时候 $M_{0,1}(Na-P)=\sum_j f_{1}(|r_{Na,j}|)*(x_{ij},y_{ij},z_{ij})=[c^{0}_{1,Na,P}(2.5-|r_{Na-P}|)^2+c^{1}_{1,Na,P}(\frac{2|r_{Na-P}|-3.3}{1.7})(2.5-|r_{Na-P}|)^2](x,y,z)+...=[c^{0}_{1,Na,P}(2.5-1.414)^2+c^{1}_{1,Na,P}(\frac{2.828-3.3}{1.7})(2.5-1.414)^2](1,1,0)+[Na-O]+...$

得到一个长度为3的矢量，和angular一样

level OF MOMENT tensor

\[lev[M]=2+4\mu+v\]

这个是MLIP的level,可见随$\mu$增长很快,在v是0情况下,v=0时候level是2,v=1 (也就是说,有两组radial part)的level就已经是6了.

Basis functions

basis functions 和 moment tensor 在定义上面不同在于，moment tensor 可以是标量也可以是矢量，但是basis function 必须是标量。 basis function可以是本身就是标量的moment tensor , 也可以是两个矢量moment tensor通过一些运算（例如点乘）组合成标量。这个限定条件在MLIP文章里面没有，在另一片文章里面（Accelerating high-throughput searches for new alloys with active learning of interatomic potentials）

\[B_{\alpha}=M_{\mu,v}\]

basis function 如果直接是以单个的moment tensor 来表示的话，level计算和moment tensor当然是一样的当进行组合的时候例如

对于本身就是标量的moment tensor，可以互相相乘组成新的比如说对于$M_{0,0}$, angular part是常数1，这个moment tensor是个标量。那么自己与自己相乘得到一个新的标量 $M_{0,0}*M_{0,0}=M_{0,0}^2$

$M_{0,0}$的level是$2+4*0+0=2$ $M_{0,0}^2$的level是$2*2$， $M_{0,0}^6$的level是$2*6=12$

对于本身是矢量的moment tensor，可以取向量点积得到一个标量的basis function 比如说对于$M_{0,1}=C_1r_{Na-P}+C_2r_{Na-O}+...=C_1(x_{Na-P},y_{Na-P},z_{Na-P})+....$ 这里用C来省略radial part 这是个矢量那么 $M_{0,1} \cdot M_{0,1}= [C_1r_{Na-P}+C_2r_{Na-O}+...] \cdot [C_1r_{Na-P}+C_2r_{Na-O}+...]$ $=C_1^2r_{Na-P}\cdot r_{Na-P}+2C_1C_2r_{Na-P}\cdot r_{Na-O}+C_2^2r_{Na-O}\cdot r_{Na-O}$ $=C_1^2\vert r_{Na-P}\vert ^2+2C_1C_2 \vert r_{Na-P} \vert \vert r_{Na-O} \vert cos(\alpha _{P-Na-O})+.....$ 这重新变成了一个标量点乘的时候，level是相加的这个的level 是 $(2+4*0+1)+(2+4*0+1)=6$
对于矩阵，可以求frobenius积这个是两个相同形状的矩阵对其每个同位置元素相乘后求和此操作同样是导致level相加

total energy

$E=\sum_i V(n_i)=\sum_i \sum_{\alpha}\xi_{\alpha}B_{\alpha}(n_i)$

cluster expansion

比如说这样一个lattice

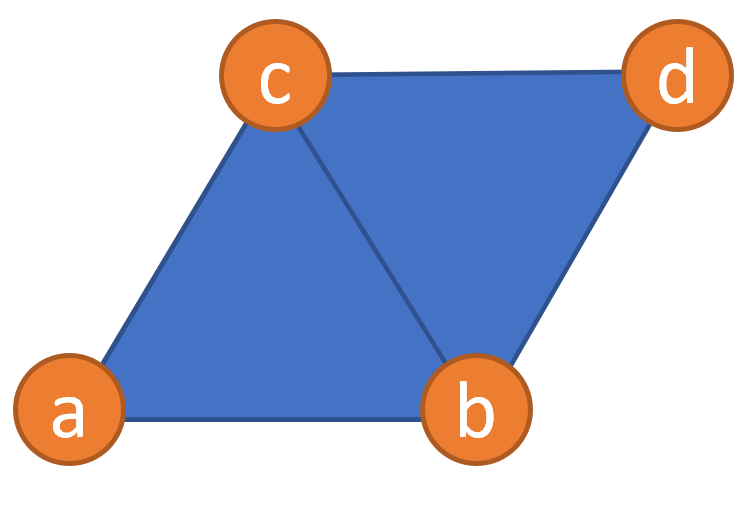
site: 一共有4个site， a,b,c,d
state 总共有$2^4=16$个state
occupation variables $\sigma_i$: 在site i上面的occupation 例如在a上面有occupy的原子，则$\sigma_a=1$
occupation vector $\vec{\sigma}$ $\vec{\sigma}=(\sigma_a,\sigma_b,\sigma_c,\sigma_d)$ 例如在state0下面的occupation vector是 $\vec{\sigma_0}=(-1,1,1,-1)$
cluster: $\alpha$ 比如，单个site可以是一个cluster 两个比较近的site可以是一个cluster 例如$\alpha=(a)$ $\beta=(a,b)$ $\gamma=(a,d)$ $\delta=(a,b,c)$
cluster function $\sigma_{\alpha}(\vec{\sigma})=\prod_{i\in \alpha}\sigma_i$ 例如对于$\vec{\sigma_0}=(-1,1,1,-1)$ $\sigma_{\alpha}(\vec{\sigma_0})=\prod_{i\in \alpha}\sigma_i=\prod_{i\in (a))}\sigma_i=\sigma_a=-1$ $\sigma_{\beta}(\vec{\sigma_0})=\prod_{i\in \beta}\sigma_i=\prod_{i\in (a,b))}\sigma_i=\sigma_a*\sigma_b=(-1)*1=-1$ $\sigma_{\delta}(\vec{\sigma_0})=\prod_{i\in \delta}\sigma_i=\prod_{i\in (a,b,c))}\sigma_i=\sigma_a*\sigma_b*\sigma_c=-1*1*1=-1$